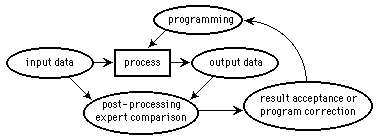
Figure 5: Program creation and testing
The next step is to investigate the implications of our set of guiding descriptives in the structural or dimensional context of space and time. We need to look at the relationships between Experts and Programming, between Data, Control and Physical Structure, the Character of the Processing itself, and the usual Requirement for Inversion.
In conventional computation, the processing depends on a predetermined set of sequential instructions or a currently applicable set of rules. Successful programming or rule design is confirmed by more or less complete testing; the program is run in a controlled environment, and the relation between inputs and outputs is checked by an expert in the field (figure 5). If the relation is satisfactory the program is accepted, and if not then it is corrected and re-tested.

Figure 5: Program creation and testing
Unfortunately, the same kind of expertise appears here twice, once in the programmation and once in the acceptance procedure. This brings with it great accuracy in areas which are closely related to the testing procedures, but the imposed consecutive assumptions that (1) the physical structure of the computer is error-free, and that (2) the program controlling the data manipulation is error-free, are in some cases catastrophically destructive of accuracy. In such (commonly occurring) cases a controllable degree of normal uncertainty would be much more acceptable than normally high accuracy and occasional disaster. Small errors are more user-friendly than large ones!
The data-transport medium and the control-transport medium should at the very least be capable of bi-directional interaction. Classically, the application of control results in data-manipulation, which generates new data, which through conditional jumps can influence the control. If the data- and control- transport media are identical, then in the absence of a physically structured environment constraining their interactions the data and control are indistinguishable. Ideally, in a data-based structure, control and static architecture should be integrated into a purely dynamic form which disappears in the absence of data.
The requirement in relational operations for conservation of data redefines this processing as a rearrangement of existing data. In the simple example of a planar pixeled binary image which passes through a processing plane to give a new planar pixeled binary image, the total information present in each of the two image planes must be the same. Any required pixel in the output plane must then be derived from a possibly spatially unrelated pixel in the input. This requires non-local connection between all of the input/output pairs in the processing plane, or totally distributed processing. This is illustrated for a simple one-dimensional case in figure 6, where the input and output images have each 20 pixels. The input plane has 60 units of information equally distributed, and the output is the result of some arbitrary processing function; the total information present in the output is the same as that in the input. In such a scheme individual inputs and outputs are no longer uniquely linked, and the complete image must be processed in a unified manner. It would not appear possible to carry out such an operation using discrete pixelated processing elements or devices.
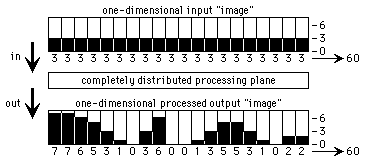
Figure 6: A simple distributed processing example
In such a distributed processing plane the correctness of the resulting pixel array depends on the number of input/output pixel pairs. The probability of being able to generate a totally correct output array for any arbitrary processing function increases rapidly with the number of pixels involved. With only one pixel in each of the input and output there is only one possible processing result; some functions will require forward transmission of the input pixel, which is always available, but others will require inversion, which is impossible. Even with large pixel arrays, there is the possibility that output information densities will be required which differ from the input densities, but such cases appear always to be associated with decision-making processes and not with interrelationships.
The combination of large-scale totally distributed processing and data-conservation removes the usual computational requirement for discrete inverting devices. Inversion is only required if lateral processing access is limited, as is the case for conventional Boolean gates and discrete-neuron neural networks.
A simple if very restricted example of discrete element distributed processing is provided by a winner-takes-all circuit, as shown in figure 7.
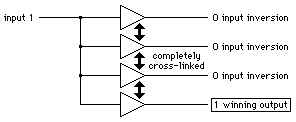
Figure 7: Simple distributed processing in a ``winner takes all'' circuit
The input summation must rise above the circuit's threshold value, the output
summation
is fixed at unity, and the processing-plane must be completely laterally
connected
for the circuit to operate correctly.
The winning output is equivalent to a (possibly scaled) forward transfer
of the
input, and all the other outputs give an inversion.