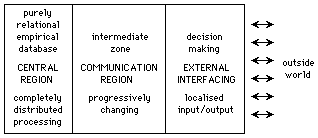
Figure 8: Communication between the central region and external interfacing
The desirable decomposition of computation into interrelational and decision-making processes presupposes an intermediate structure capable of linking the two in a bi-directional manner (figure 8).

Figure 8: Communication between the central region and external interfacing
For the moment we will leave aside consideration of this intermediate communicating structure and concentrate on the characteristics of the central database region.
The primary requirement for the central region is that it should have the character of a purely empirical database, with totally distributed data-conserving interactions, no decision-making processes and no thresholding, which appears to imply a completely chaotic structure. This conclusion, however, presupposes the absence of defined boundary conditions.
The presence of chaos or of explicate order (structure) [1] in a given environment will depend on the boundary conditions themselves, where these are defined in the most general terms and not solely spatially. The imposition of suitable conditions on such a data-assembly should of itself result in the development of structures in the internal interactions which may be interpreted as models by the more decision-based environment of the communicating intermediate zone.
An obvious boundary condition is the relation between the information content of the total dataset and the information capacity available. Data must in some way be squeezed into the central region to avoid dispersion and loss of interaction intensity. This also implies that the database region must be capable of growing as the total dataset increases in size.
Instead of mapping raw data into the central region, it is interesting to consider the possibility of filtering all datasets through their corresponding models and storing only the model-misfits in a distributed processing database. This would enable the generation of modeling of as-yet undescribed global phenomena, which can then be used to correct existing data descriptions and reclaim data in terms of a unification of modeling success statistics instead of using the specific dataset/model relations on their own.
Returning now to the intermediate communicating structure, we propose a query-reflection architecture capable of linking the central region to the necessary external interfacing. This structure also has wider implications, in that it is applicable to future development of current expert systems.
The intermediate zone will resemble a pyramid of rule-levels linking an extensive database (the pyramid base) to a single outside point (the pyramid summit), as shown in figure 9.
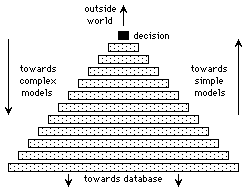
Figure 9: Model complexities in a rule-base pyramid
Viewed simplistically, each level consists of a set of rules describing a model, which is itself derived from a more extensive rule-set one level farther down, and which enables the derivation of a smaller rule-set or simpler model one level higher up. The closer to the database the more individual rules there are, and the closer the rules are themselves to simple data descriptions where fewer approximating assumptions are made. This means that the models become simpler and their constituent rules are representative of more data on moving up the pyramid. In this context the extreme form of a model is just a decision, so the structure corresponds to the requirement of linking data at one end to decision-making at the other.
A simple example of such a multi-level arrangement is that of the sequence of models which are used to describe the v-i characteristics of a p-n junction diode, labelled from 1 to 6 in figure 10.
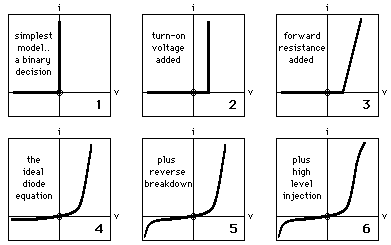
Figure 10: The p-n junction diode model sequence
The simplest model (1) is a binary decision, with perfect forward
conduction and
perfect reverse insulation.
Each model level (2, 3, ...) adds parameters and complexity while approaching
more
closely an exact equivalence between the model and the complete available
dataset.
An even more complex model further down the sequence would also include the
statistics
of the differences between the empirical and deterministic model values.
Ideally, the model values corresponding to the most complex form would exhibit
the
same statistical properties as the empirical data, which corresponds to a
model-misfit
mapping description of the storage of a big zero.