Figure 2: Activity Thresholds in complex situations
It is possible to formulate empirically a number of useful guiding descriptives for intuitive computation. These include the idea of Activity Thresholds, the difference between Relationships and Decisions, the requirement for Reversible Processing, and qualification of the Prediction of Data.
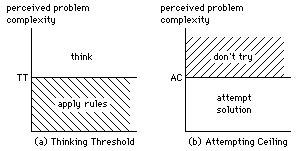
In perception/computation situations there appears to be a level of perceived problem complexity, or Thinking Threshold, below which pre-learned or defined rules are automatically applied, and above which an attempt at a solution is made by more complex methods (figure 2a). Rules can only be applied if they are known: traditionally the level of rule-knowledge has been partially equated to intelligence, as in intelligent people know how to do a lot of things.

Figure 2: Activity Thresholds in complex situations
There also appears to be a level of perceived problem complexity, or Attempting Ceiling, above which there is an inability to approach a solution on the basis of currently accessible tools (figure 2b). The level of this ceiling has also been partially equated to intelligence, as in intelligent people can deal with complex problems.
Overlap of these two Activity Thresholds suggests that rules are applied whatever happens, and there is no capacity for relating the rules to the current context (figure 3a). This results in the application of rules in inappropriate situations, such as the safest way to cross a road in England is to first look to the right, so this must be the case in France as well.
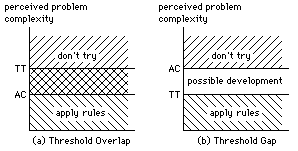
Figure 3: Restrictive and non-restrictive Activity Threshold combinations
A gap between the two Thresholds implies that there is a range of perceived complexity for which there is the ability to use rules where they are appropriate, to derive new rules where possible, or otherwise to continue by extended data manipulation (figure 3b). We should expect extended capability to be associated with the presence of a very big gap, as this implies that there is a wide range of perceived complexity within which there is the capacity to attempt rule development. A gap of this kind is then a primary criterion for an intelligent computer, but the advantages of the availability of a rough and ready set of simple easily applied rules should not be neglected; it is faster to use an available rule than to search for a more exact relation to an empirical situation. This equivalence to the phenomenon of rapid reflexes in animals should be included if a machine is to work in a real-time environment.
The result of environmental-reaction computation is usually some kind of decision, in its simplest form a binary yes or no. This can only be arrived at from data by a style of processing which reduces or effectively destroys the data on the way: such a process is not reversible. Boolean logic itself is a case in point, and as such is less than ideal for large-scale interrelational processing. In the Boolean AND gate example of figure 4, if the output column Z is removed from the truth table then it can be reconstructed correctly from the two input columns A and B if the nature of gate (AND) is known; such is not the case if either of the input columns A or B is removed; this is characteristic of an irreversible process. It seems a good idea to partition a processing machine into two distinct areas, one for data-conservational relationing, and one for data-destructive decision-making.
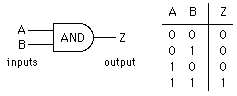
Figure 4: The irreversible nature of the Boolean AND operator
The idea of modeling is to use current data to visualise the real nature of an effect, but this can never take account of whether a model will satisfy data in as-yet uncharted regions. The statistical relation between a dataset and its own corresponding model is therefore not sufficient for data prediction, and the relation should include an indication of the success of the generalised modeling process itself, which would require interaction between the statistics of all available dataset/model environments. This clearly implies the use of massively-scaled databases where the different datasets are in some way integrated.
The usual approach is to propose a model for a given situation and then to test
it using
currently available data.
A more useful technique would be to allow the local data to interact with other
datasets to
autonomously generate a suitable model.
A problem here is that the usual acceptance of a model in terms of
simplistic
sufficiency is left out, and so the model complexity must in some way be
related to the
requirements of the context.