If all successive reflections in the multiple query-reflection structure are
exactly the same,
then the simplest model is a perfect representation of the entire available
dataset.
If successively appearing reflections R1, R2, ...
differ, then the nature and magnitudes of the differences 
R12, 
R23, ...
describe discrepancies between their respective model-layers.
This is illustrated in figure 14,
where the relation between query and reflections is described in terms of time (vertically) and the model dimension (horizontally), which is related to distance through the structure. If the model layers are such that reflection is possible in both directions, then the multiple reflections themselves will be reflected back inwards, giving rise to information summations which correspond to summed inter-planar model differences. This permits correction of the model-layers themselves: as these are built up from the data level by progressive rule combination the resulting inter-planar oscillation of information can be used to modulate the layer reflectivities. Adjacent models will then also be correlated.
There are two major problems in modeling the interactions. Firstly, that of propagating data through relational knowledge, which means that data is mapped onto other data by relations and not by functions, and secondly, of propagating the data back again to check and update the database, which can be done by inverting the relational knowledge.
Two mathematical representations present themselves.
We can describe the queries and reflections as the interactions of propagating
waves with
the model-layers.
These interactions are partial reflections characterised by 
and
in
figure 15.
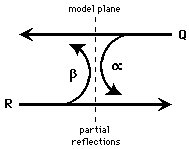
Figure 15: Propagating wave representation
It is also possible to describe a structure of this kind in terms of interaction centres, with information summation at the centres followed by re-emission (figure 16).
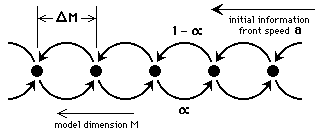
Figure 16: Interaction centre representation
In the limit of the difference between successive model-layers tending to zero the two formulations are equivalent, and may be described in a pseudo-one-dimensional equation by
where
,
,
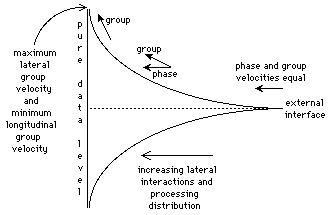
Figure 17: Information group and phase velocities in Aquarium
This means that the so-called central database is completely inaccessible!
A more realistic description of the combination of database and query-reflection region is that the one progressively changes into the other through the model-layer sequence, and that the data is distributed into the query-reflection structure itself. Progression towards the data base end is equivalent to filtration of incoming data through the successive model-layers, and it is only the model-misfits which will be eventually left over as a central non-deterministic chaos.
Decision-making consists of choosing one of a set of relevant decisions on the
basis of a
dataset and previous experience (knowledge).
Every possible decision receives a confidence factor (or probability)
that it is the
best solution to the problem.
Working with classical probability is frustrating in this case, as the
knowledge must be
built up in such a way that every data element corresponds to only one
decision.
If (as usual) this is not the case, rules are required to distribute the data
confidence factors
over their associated decisions, but it is now impossible to find one-to-one
correspondences and a lot of practical problems result.
As an example, consider a set containing 1,000,001 possible decisions of which
1,000,000 are associated with a single data element.
A possible rule for distributing the element's confidence factor is to give
each associated
decision the same confidence.
If the element's confidence factor is 99%, then each of the 1,000,000
decisions has a
confidence of 
%, but the single unassociated decision will have a
confidence of 1%, making it the best decision!
There are different ways of tackling this problem. We can assign weights to subsets of a set instead of allocating confidence factors to each element [2,5]. This allows us to calculate the upper and lower probabilities of each element. In the example above, each of the 1,000,000 associated decisions would have a lower probability of zero and an upper probability of 99%, but now the unassociated decision would have a lower probability of zero and an upper probability of only 1%. The selection of best decision would be now very different, and more correct. There are still some problems remaining with this approach [6]. We have a strong belief that this is due to the fact that the theory of Dempster/Shafer is working with discrete elements and discrete mappings between them.
The architecture presented in this paper has by its nature a continuous data
input set
(which varies continuously over time) and a continuous representation of the
knowledge
(the contribution of the data to a decision can be changed continuously by a
model).
In equation 1 the reflection factor 
is the confidence
factor that
the model M delivers the best decision.
Relational and decision-making processes may be represented by linear and sharp-threshold transfer characteristics, as shown at the two extremes of figure 18.
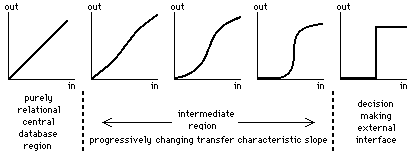
Figure 18: Progressive change of the processing transfer characteristics through
Aquarium
The proposed structure, Aquarium, must progressively change in character
between the
two extremes, and this change may be represented by a threshold-control
function
which depends locally on the inter-model-layer difference 
and is
obtainable
through 
from the local bi-directional reflection summations.
A plot of the maximum transfer characteristic slope against the inverse model
complexity
is shown in figure 19.
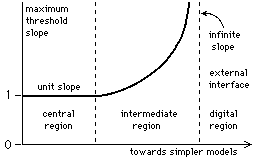
Figure 19: Central region localisation of the model-filtered data
The remaining model-filtered data (the model misfits) are restricted to the
central region
in a manner which resembles the localisation of particles within a potential
well (which are trapped).
We believe that autonomous threshold-control can provide the boundary
conditions
necessary to force the generation from chaos of data-``structures'' which may
be
recognised as models by more decision-based processing.
