Humble Unification Theory:
Partial Comprehension in a Quasi-Particulate Universe

Ron Cottam, Nils Langloh, Willy Ranson & Emilie Cottam

Download as

Zipped RTF document for MSWord etc.

Introduction

            It is possible to represent the dynamic nature of the understanding of our surroundings in a way which is similar to the scientific description of reactionary phenomena, with regions of stability corresponding to general acceptance of currently formulated perceptions, and regions of instability which give birth to the evolution of dramatic comprehensional phase changes [1] in which previously stable perceptions are modified, replaced or annihilated. Chris Langton [2] has argued that one of the major uses of the study of artificial life is as a way of evaluating the feasible resultant footprint of evolutionary development without having to locally assess the implications of all possible adaptive branching processes. Concurrently with the development of these ideas there is a move towards the reformulation of evolutionary principles in a manner more consistent with the results of investigations into emergent computation ** [3]. The intention of our work is to draw together these and a number of other strands in formulating a new overall framework capable of supporting not only the reductionist scientific description of nature, but also the implications of an evolutionary recombination.

            We describe a computational model which is consistent with the presupposition that survival by the maintenance of organisational integrity is the main individual aim of living entities. The principal survival criterion can be described by the relationship between the time-scale of an internal reactive process and that of the external reaction-demanding environment, and evolutionary success becomes primarily a question of ensuring phenomenological computability. This corresponds well with propositions [4] that the critical slowing down associated with phase changes can be attributed to an inability of the constituent media to "compute" sufficiently rapidly their equivalence to the parametric representations implied by the changing states, and brings into focus Bohm's [5] universal metaphor that all recognisable entities are alive and conscious to a greater or lesser degree. Survival requires the prioritised identification and objectivisation of dimensions within which an entity is most fragile or most at risk [6]; the evolutionary co-development of a selectively-dimensioned environment [1] brings with it enhanced computability and consequently competitive advantage.

            Timely computation of an entity's reactions to unpredicted environments necessitates the availability of simplified representations of the interaction between an entity and its surroundings in their combined multi-dimensional phase space. Meta-states characterising these objectivisations correspond to regions of the phase space where its contextual description can be reduced reasonably accurately to a small number of parameters or degrees of freedom, and they are equivalent to the visualisable limited-parametric provisional stages of an evolutionary computation. The inter-balance between communication and order required for the development of transient trial solutions to environmental problems [6] can be re-described in terms of computability: applicable models must be available or developed within the time permitted by the context. Simple models permit rapid reactional computation, but accurate representation is necessary for detailed evaluation of an environment. Fortunately, these mutually-contradictory requirements are normally not in play simultaneously.

            Historically, the most effectively transferrable symbolic model has been that of conventional logic, whose success can be documented through the progressive rise of deterministic science and technology. Starting from our description of adaptive real-time environmental-reaction survival computation in a natural temporally-demanding medium [7], we develop a more general model of the evolutionary context itself as a computational machine [6]. The effect of this development is to replace deterministic logic by a modified form which exhibits a continuous range of dimensional fractal diffuseness between the isolation of perfectly ordered localisation and the extended communication associated with nonlocality as represented by pure causal chaos. A consequence of this replacement is that the inter-dimensional coupling required to maintain universal coherence naturally has a form which can support the integration of irreversible history and therefore evolution into otherwise deterministic science.

            Implementation of these ideas into a mathematically manipulable scheme depends on the extension of current mathematical practice to deal with less than deterministic contexts. It is not sufficient to resort to classical probability or even fuzzy logic; we must model the natural inter-dimensional diffuseness as a way of characterising the emergence of new models from unfamiliar data. This is evidenced by the difficulties encountered in maintaining logical completeness in the extension of a quantum mechanical treatment to large systems [8]. In a computability-based representation of evolution situated between determinism and chaos, the difference between chance and complicated multi-dimensional determinism becomes blurred, and we must replace classical ideas of probability by a more contextually aware formulation closer to that derived by Dempster and Schafer [9, 10] for discrete sets.

An Adaptable Real-Time Processor

            We can obtain processor response satisfying the double requirement of fast and accurate environmental responses by using a query-reflection structure [7]. We arrange a suitable hierarchy of models organised into a series of reflecting planes, as shown in figure 1 with the simplest at the right and the most complicated one at the left. When we fire a query at the structure the immediate reflection is from the simplest model, so the response to the query can be very rapid. The second reflection is from a model which is more complicated, so its processing demands more time. Progressively the successively returned reflections take longer and longer to appear, but they are more and more accurate with elapsed time.



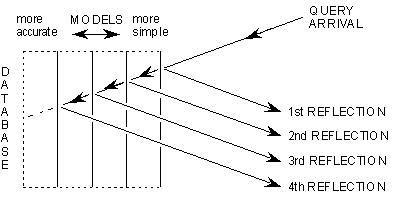
Figure 1: Multiple reflections in a query-reflection structure, showing the availability of both fast and accurate responses.

            Decision-making usually proceeds by the reduction of an available (large if not complete) dataset through progressive applications of sets of rules to a final binary conclusion. In its most simple form this has the shape of a pyramid (figure 2) with the database as the pyramid's base and the decision at the apex. Towards the database end of the structure the rule sets are extensive, but each rule is fairly closely related to specific localised parts of the empirical dataset itself, whilst towards the decision end the rule sets are much more compact, and the results of rule application involve rather gross approximations to the now distant empirical data.



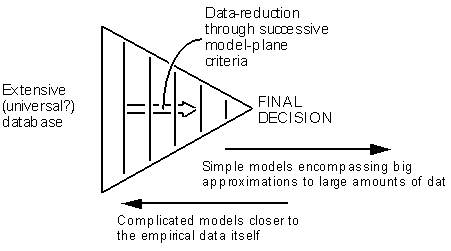
Figure 2: Decision-making by data-reduction through sequential criteria.

            Combination of the query-reflection idea with pyramidal decision-making gives us the basic form (figure 3) of an adaptable real-time processor ["AQuARIUM": 7]. Data-resembling queries propagate from right to left, provoking data-like multiple reflections from the sequential model-planes in the body of the structure. Recursive inter-model-plane reflections stabilise the relationships between consecutive model-planes, resulting in a coherent progressive change between the simplest and the most complicated data representations.



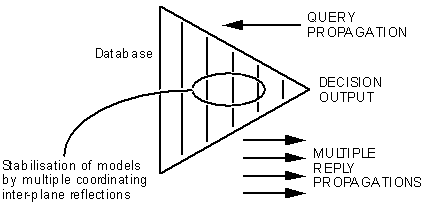
Figure 3: Combining query-reflection and pyramidal decision-making.

            The data is not now confined to the originally described database at the left hand side, but is implicitly distributed throughout the model-plane assembly in the associated rule-sets. Incoming queries are progressively filtered through the sequence of continuously-restructuring more and more detailed representations, until only the residual non-fitted parts remain. By waiting as long as possible we can obtain the best response feasible within the time available; but now there is a problem. It is the external stimulus itself which defines the permitted response time scale, and as the "lateral" query velocity must increase as the size of the accessed dataset increases (figure 4) we finally run out of "longitudinal" query (group) velocity, and model-planes at the extreme left hand side become completely inaccessible. This restriction is similar to that imposed in free-space communication by the limitation on the speed of light, and corresponds to the extension of velocity-related relativity to processes in any domain which is described in terms of reactive-computability.



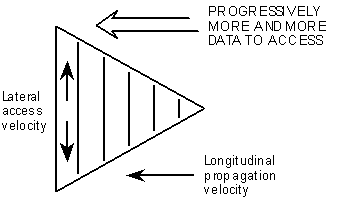
Figure 4: Query velocity limitation resulting from increasing lateral data access.

            This computational structure presents a number of interesting similarities to and differences from conventionally described neural networks. Recent neurobiological research [11, 12], indicates that the human brain also makes use of a selective-precision reactional system, with the amygdala providing access to both rapid response (from the thalamus) and accurate representation (from the cortex). The cortex pathway involves many more neuron-to-neuron transitions, and is much slower than the thalamus path. The transmission of a query through one of our model-planes involves lateral communication in the plane itself as a way of sensitizing the query to all of the data available at that model-level. This is reminiscent of the lateral diffusion of messenger chemicals (for example nitric oxide [13]) from target synapses to the physically adjacent synapses of other neurons, which may be linked to the implementation of the population coding of perceptional features [14]. Conventional neural network descriptions only take into account uni-directional neuronic information propagation, although the validity of this supposition for the brain is now in question, with the discovery of fast antidromic spikes transmitted from the axon hillock back towards the synapses [15].Our model relies on local bi-directional communication to globally stabilise the entire model-system, in the same way that antidromic spikes may provide the basis [16] for differential Hebbian learning by inter-neuronic correlation without requiring explicitly long-range back-propagation [14]. Recently, communication has been observed in real tissue between adjacent glial cells [17]. Is their function in this context merely to remove neurotransmitter chemicals from the synapses, or is this removal itself part of slower and more long-range communicative processes we might expect to find towards the left hand side of the reactive computational structure we describe?

A Transferrable Computational Model

            We can extend this albeit crude computational system into not only a useful model for information processing, but also finally into a generalised description of the evolutionary appearance of localised entities in a universal context, as in figure 5. The imposition of a perceptional system on information processing implies the reduction of possibly unstructured information to a structured perceivable form related to symbolic representation. We construct the representation on the basis of "capability for communication" as the primary parameter and not on energy, which now becomes a dependent parameter, and the model-planes which appear in the computational description as stabilised partial computational results are functionally equivalent to the meta-states which are found in the evolution of complexity. We include explicitly the necessary condition of a "real" communication limit for the existence of causality in any environment [18], and the database itself consists of all the data which can have been generated by previous queries and reflections.



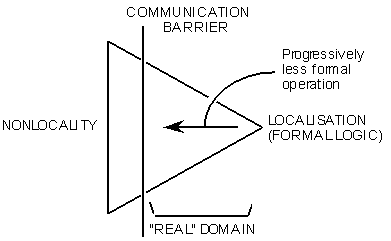
Figure 5: The general symbolic representation of evolution through computation.

            In the resulting symbolic representation of a generalised environment shown in figure 5, an equivalence is made in the longitudinal direction between {pure communication, pure nonlocality, complete disorder and pure "causal" chaos} at the left hand side, and between {complete lack of communication, complete localisation, complete order and degenerate formal logic} on the right. By concentrating on the overall complementary decompositional and reconstitutional aspects of nature as we observe it, and not on the primarily reductionist picture that classical modeling would suggest to be the most applicable, a number of difficult empirical aspects such as communication become easier to handle, and in some cases even of fundamental importance.



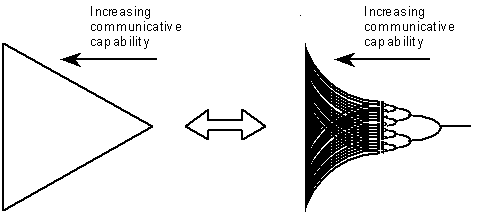
Figure 6: A comparison between the forms of query-reflection and the logistic plot.

            The "real" domain now spreads from the imposed communication barrier to the pyramid apex on the right, and movement from the apex in the direction of the left hand side is equivalent to a progressive change away from formal logic into a more partially rational state. Regions towards the left correspond to a higher capability of communication, but not necessarily to an increase in communication itself: the emphasis here is on describing environments in terms of "capability" and not "property".



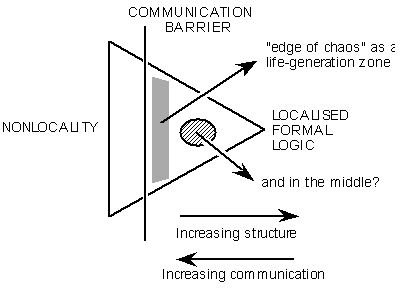
Figure 7: Location of the edge of chaos region in the symbolic representation.

            The similarity between this symbolic representation and the simple chaotic logistic plot shown in figure 6 is not accidental: both are describing the same relationship between unstructured information and its structured representation. Nicolis [19] has pointed out that chaos enables a system to explore its phase space, which corresponds to the necessary in-plane data access required for the model-assembly stabilisation described above. "Deterministic" chaos seems to be nature's best attempt at penetrating an imposed communication barrier, and it represents a meta-model of the underlying "causal" chaos equivalent to communication itself. If we now add chaos itself into the symbolic description of figure 5, we can identify the location of Langton's [20] "edge-of-chaos" some way to the right of the causally-imposed communication barrier (figure 7) , and necessarily far from the apex which represents formal (closed boundary condition) logic. This region exhibits the balance between communication (towards the left in our representation) and structure (towards the right) necessary for the evolutionary germination of complexity [20] and in all probability "life" itself.

A "Psychological" Potential Well

            To evaluate characteristics of the region to the right of the "edge-of-chaos" we must first of all make a short sideways step to look at how we ourselves react to different degrees of perceived complexity in our environment. Below some arbitrary level of perceived complexity (the "thinking" threshold) we make blind use of pre-existing rule structures (figure 8a), and it is only when our perception of the complexity of a situation passes this threshold that we begin to "think" about how to deal with the situation. Above a certain level of perception of complexity (the "attempting" ceiling) we no longer have the formal mental tools available to approach solution of a problem (figure 8b), and we abandon the attempt or try non-formal methods.



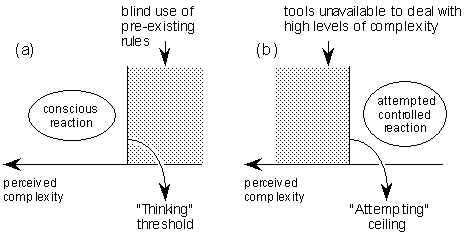
Figure 8: Reactions to differing perceived complexities: (a) the "thinking" threshold, and (b) the "attempting" ceiling.

            If when we superimpose these two phenomena the shaded regions shown in figure 8 overlap, then there will be no ability to adapt rules to new situations, and the result will be a set of more or less stupid responses to the environment. If, however, there is a gap between the two, this implies that there is a region of perceived complexity within which there is the capability to react in a consequent manner to the context in which we find ourselves: this is a necessary condition of, and result of, consciousness itself, and we can locate this "consciousness-capability" gap in the general symbolic model as shown in figure 9. Evolutionary growth of this "consciousness-capability" gap appears to be equivalent to the development of "life" as we conventionally describe it. This would be the case not only for "living entities", but for all perceptional localisations, consistently with, for example, David Bohm's assertion [5] of the (presumably) low-level "consciousness" of electrons.



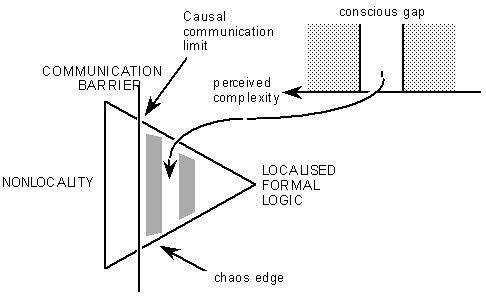
Figure 9: The appearance of a "consciousness-gap" adjacent to the chaos edge.

            The development of localisations of this kind demands evolution along the lines proposed by Szamosi [1] as a modification of Darwin's proposals, in which a dimensional domain evolves into reality coincidentally with the dimensionally-embedded structure itself. It is reasonable to suggest that the dimensions which would become the most perceptionally organised (or objectivised) would be those in which the developing structure is the most fragile, viz. apparently in space and time. we could expect a gap to develop in both width and depth (figure 10) to constitute a containing "psychological potential well" for consciousness, centred around the "easiest" or "most-computable" representational form of an approximate Newtonian objectivisation.



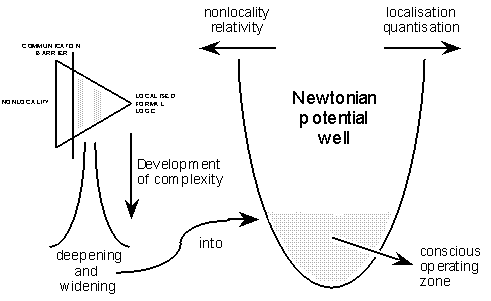
Figure 10: Widening of the consciousness-gap into a Newtonian potential well.

Nonlocality and Quantised Perception

            We propose that comprehension itself can be looked upon as the localised result of a "survival"-type computation, and consequently that it can be treated as a quasi-particle, similarly to all other (real) localised entities. Quasi-particle emergence and stabilisation in this scheme consistently depend on "local" criteria, as for electron-positron emergence in "free space". If this description is valid, we should expect to see the "materialisation" somewhere in large-scale neural computational structures of extremely localised high-level perceptional representations of environmental features. It may be that there is an intimate link between this expectation and the emergence of semi-autonomous activity "bubbles" [21] in continuum neural field theory modeling of the brain.



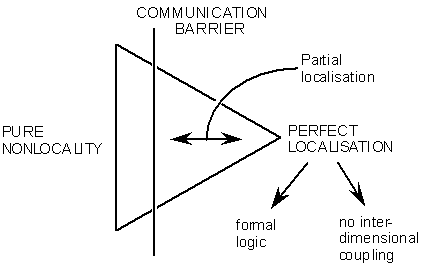
Figure 11: The appearance of partial nonlocality in the "real" zone.

            The modified evolutionary description fits in well with super-string models [22], where there is the requirement for auto-generation of space and time. Nonlocality appears in this context as a description of perfect communication, and as such it also appears in the real zone in a partial manner (figure 11), rather than remaining an esoteric phenomenon uniquely associated with quantum physics.

            It is clear that we always operate in a state of only (time-averaged?) partial comprehension, where the use of formal logic without the support of firmly defined environmental boundary conditions can be confusing or contradictory, if not plain catastrophic! This is precisely the region in which large-scale digital computer systems can operate in their most disastrous manner if account is not taken of the possibility of unforeseen operating conditions. We can gain vital survival-related advantages by using processing styles which replace the absolute un-scaled precision of binary-rational computation by more context-aware formulations. In an investigative situation we often experience other than partial understanding, for example on finding a new and apparently bounded model which provides a universal description of reality, but this is soon replaced by reversion to the realisation that we still did not "describe it all". Grand Unification Theories are here a case in point, because however accurately they may describe the existence and interaction of elementary particles and forces, they do not contain the elements necessary to rebuild the world which has been disassembled to create them.

            An important feature of our current description is that it does not suffer from this problem: nowhere do we suggest that parameter-carrying transformations to all domains can be carried out; only that the general form of data-integration will remain the same. This makes it vitally necessary to apply a "correct" mathematical approach to describing inter-dimensional effects, as the resulting characteristics will be carried over into all domains into which we transfer the model framework. We are most concerned with modeling relationships and not simply functions, and here classical probability suffers from a lot of difficulties, particularly if the relations are not simply one-to-one. A better approach is to use upper and lower bounded probabilities as described by Dempster [9] and Schafer [10], where there is no imposed "deterministic" central value to the range of probabilities describing an event. When this probabilistic conversion is carried out in a recursive manner, it is capable of generating the diffuseness [6] associated with a progressive change from localisation towards nonlocality in a multi-dimensional system.



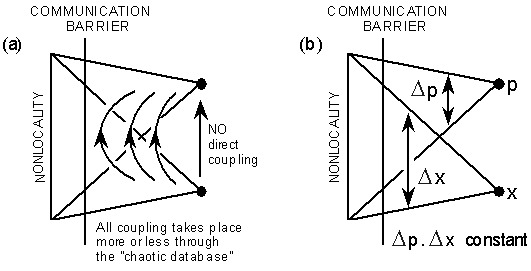
Figure 12: Inter-dimensional coupling is: (a) never direct, but only through the "chaotic" database, and (b) consistent with the limitation indicated by Heisenberg's uncertainty.

            Coupling between different localised dimensions in this scheme always takes place more or less through the "chaotic" database (figure 12); there is no coupling at all directly between completely localised dimensions, and consequently dimensional interactions are always to some extent irreversible. Heisenberg's uncertainty principle appears as a special case of coupling between two dimensions which are linked by a constant coupling factor: if one dimension is completely localised, the other is completely uncoupled and therefore unknown. Note that this is only the case if the coupling between completely localised dimensions is zero.



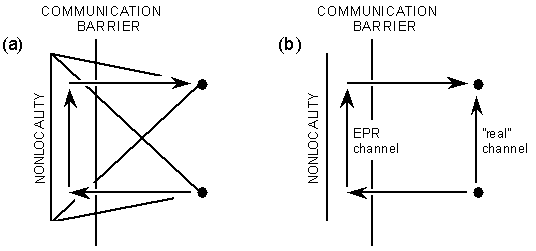
Figure 13: The computational paths implied by (a) nonlocal communication without using a "real" channel, and (b) Bennett et al's "teleportation" through combined EPR and "real" channels.

            What about the apparent possibility of coupling two dimensions directly through the nonlocal communicative background, as some sort of telepathy? Bennett et al [23] have presented a scheme for the uncertainty-free transport ("teleportation") of a quantum state between different locations through use of an Einstein-Podolsky-Rosen nonlocal channel (figure 13). Closer examination reveals this to be a single-quantum version of the more general propositions of this paper, and it is clear that it is fundamentally necessary that there is not only communication via an EPR channel, but by a "real-world" channel as well: for a "real" communicative result we still need "real" communication.

Conclusions

            The current state of understanding of the operation of real neuronic systems supports the view that our model can operate as an archetype for the computational processes which the brain emulates, and that it can be used to help target investigations into neuronic computational processes.

            We conclude that this generalised quasi-model framework, which is presented here only in its most primitive form, can describe any localised entities, including perceptions themselves. The formulation is entirely consistent with David Bohm's [24] description of nature in terms of implicate and explicate order, and the model can be transferred between different scales and domains of interest without requiring the transfer of formally localised parameter sets. The proposition of the appearance of partial or diffuse rationality with movement away from perfect localisation is confirmed by Ioannes Antoniou's work [8] on the extension of quantum mechanics to large systems, where he finds that the logical completeness criterion breaks down.

            We believe that the quantum tradition of this century can be complemented by treating comprehension itself as a quasi-particle, and similarly for all other (real) localised entities. The prefix "quasi-" then accrues a quantitative sense in terms of the degree of localisation involved.

Acknowledgments

            This work has been carried out in the context of the Brussels University (VUB) Laboratory for Microelectronics and Technology (LAMI) programme of research into advanced processing architectures, and is supported by the Inter-University Microelectronics Center (IMEC), Leuven, Belgium. Our thanks go to Erik Stijns of the Applied Physics Department of the University of Brussels (VUB) for introducing us to the thoughts of David Bohm, a former faculty member of Birkbeck College, London University, to whom this work is dedicated.

** Sections of the text above and references below which are shown in white have been added to the paper in 1997 after the Neural Computation and Psychology Workshop in London (see Conferences: NCPW-4).

References

[1] Szamosi G. The Twin Dimensions: Inventing Time and Space. McGraw-Hill, New York, 1986.

[2] Langton. C. G. Technology, nature, and the future of life. In this conference.

[3] Calvin W.H. The six essentials? Minimal requirements for the Darwinian bootstrapping of quality. J. Memetics; http://www.cpm.mmu.ac.uk/jom-emit/1997/vol1/, 1997.

[4] see, for example, Gutowitz H. A. & Langton C. G. Mean field theory of the edge of chaos. Proceedings of Third European Conference on Artificial Life. Universidad de Granada, Spain,1995.

[5] Weber W. Meaning as being in the implicate order philosophy of David Bohm: a conversation. In B. J. Hiley and F. D. Peat, editors, Quantum Implications: Essays in Honour of David Bohm, p. 440. Routledge & Kegan Paul, London, 1987.

[6] Cottam R., Langloh N., Ranson W. & Vounckx R. Partial Comprehension in a Quasi-Particulate Universe : A Framework for Evolution. In preparation.

[7] Langloh N., Cottam R., Vounckx R. & Cornelis J. Towards distributed statistical processing - "AQuARIUM: a query and reflection interaction using magic: mathematical algorithms generating interdependent confidences. In Smith S. D. and Neale R. F., editors, ESPRIT Basic Research Series, Optical Information Technology, pp 303-319. Springer-Verlag, Berlin, 1993.

[8] Antoniou I. Extension of the conventional quantum theory and logic for large systems. In this conference.

[9] Dempster A. P. Upper and lower probabilities induced by a multivalued mapping. Annals of Mathematical Statistics; 38:325-339, 1967.

[10] Schafer G. A Mathematical Theory of Evidence. Princeton University Press, 1976.

[11] LeDoux J. E. Current Opinion in Neurobiology; 23: 191, 1992.

[12] Davis M. Annual Review of Neuroscience; 15: 353, 1992.

[13] Galley J. A., Montague P. R., Reeke G. N. & Edelman G. M. The NO hypothesis: possible effects of a short-lived rapidly diffusible signal in the nervous-system. P. NAS. US.; 87: 3547-3551, 1990.

[14] Rummelhart D. E., Hinton G. E. & Williams R. J. Learning representations by back-propagating errors. Nature; 323: 533-536, 1986.

[15] Stuart G. J. & Sakmann B. Active propagation of somatic action potentials into neocortical pyramidal cell dendrites. Nature; 367: 69-72, 1994.

[16] Smith L. S. Short-term synaptic depression and antidromic action potentials. Unpublished letter, 1997.

[17] Newman E. A. & Zahs K. R. Calcium waves in retinal glial cells. Science; 275: 844-847, 1997.

[18] Prigogine I. & Stengers I. Order out of Chaos: Man's new dialog with nature. Flamingo-Harper Collins, London, 1984.

[19] Nicolis G. In ECAL 93, Self-Organisation & Life: from Simple Rules to Global Complexity. Centre for Non-Linear Phenomena and Complex Systems, ULB, Brussels (1993).

[20] Langton C. G. Computation at the edge of chaos: phase transitions and emergent computation. Physica D (Special Issue on Emergent Computation); 42: 12-37, 1990.

[21] Taylor J. G. Neural networks for consciousness. NCPW-4, 1997.

[22] Green M. B., Schwarz J. H. & Witten E. Superstring Theory. Cambridge U. P., Cambridge (UK), 1987.

[23] Bennett C. H., Brassard G., Crépeau C., Jozsa R., Peres A. & Wootters W. K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Physical Review Letters; 70: 1895-1899, 1993.

[24] Bohm D. Wholeness and the Implicate Order. Routledge & Kegan Paul, London, 1980.
______________________________________________
______________________________________________